Perfect Competition

Perfect competition is a very unrealistic market structure. We'll discuss the characteristics of it later, but for now we have to understand that it is a theoretical concept. If the world was perfect then in most cases we'd have markets operating 'perfectly'. The world isn't perfect and therefore actually seeing perfect competition in reality is a long shot. The major assumption we make is that firms are price takers. By this we mean that each firm alone has no influence over the market price because of their relative size. They take the price they can get as given and perceive it to be constant. Therefore the demand curve for a firm in perfect competition is horizontal - the can sell as much as they want but only at the market set price. Any higher and they wouldn't sell a thing, any lower and they'd make a loss in the long run.

Here we have a typical perfect competition scenario in the short run. On the left is the market where the market price is determined by the supply and demand for the good. The firm, on the right, takes the market price as given and as their price. Average revenue and marginal revenue is the same as the demand curve because we are looking at a constant price for the good. Production takes place at the point where MC = MR, anywhere before this point and more profit can be made, anywhere after this point and profit falls. If you look at the diagram, at the point MC = MR, the average cost is below the average revenue. This means profit is available, which is shown by the yellow area. In the short run the supernormal profit will be (AR-AC) x Qe.

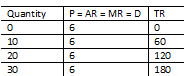
Now, above I've just said that AR and MR are the same as demand because price is constant. You want proof I hear? Sure thing. Average revenue = Total revenue / Quantity. Total revenue is actually price x quantity. Therefore average revenue can be re-written as (price x quantity) / quantity. Quantity cancels out leaving price ~ average revenue = price. Marginal revenue = the change in total revenue / the change in quantity. Substituting in what total revenue actually is we have the change in (price x quantity) / change in quantity. The change in quantity cancels out leaving price ~ marginal revenue = price. Boom!

But, we have only discussed the short run. These supernormal profits don't go unnoticed - they attract new firms into the industry. Supply now shifts out.

The price falls due to the increase in supply. On the right diagram we can see that it's fallen to the point where MC = MR = AC. This means that supernormal profit is no longer being made, it has been competed away. At this point no more firms will enter the industry because there won't be the pull of supernormal profits. Therefore, in the long run there is no supernormal profit to be made in a perfectly competitive market.

It seems risky to the normal person, producing right on the point of breaking even. This is true to a certain extent. Shocks to the system could cause demand to fall, what would happen to the firm then?

Here we have the case of a fall in demand in the market causing a fall in price. The firm was initially producing where MC = MR = AC, but now the fall in price means that if they produce at MC = MR they will actually be making a super-normal loss. This point would be below average costs and therefore the enclosed area on the right hand diagram would be loss. Would they carry on producing? Surprisingly, yes, in this case the firm would. To understand this we have to look at the breakdown of the costs. In the short run we know capital is fixed and labour is variable. Therefore the average variable cost for the firm in a simple world would be labour costs / quantity. As long as the average revenue (demand curve) is greater than the average variable costs then the firm will continue producing. This means they can cover the costs of labour and make some contribution to the fixed costs. If they couldn't cover the average variable costs it would be better for the firm to stop producing, lay off all the workers and only lose the fixed costs.

Some other things we can state is that the short run supply curve for a firm in a perfectly competitive market is the marginal cost curve until the point where price equals average variable cost. As we said above, below that point the firm will stop supplying the market. In the long run the firms supply curve is horizontal at the minimum average cost.

All we need to do now is sum up whether perfect competition is a good thing. It definitely has its advantages, they are as follows:

·         It's efficient - production occurs at the lowest average cost which is the most efficient point.

·         Competition - competition in an industry forces firms to be more efficient.

·         Price is influenced by demand - the market is essentially run by consumers, it responds to their behaviour.

·         No supernormal profits in the long run.

It really has few disadvantages though. You could state the fact that it isn't realistic as a disadvantage, I guess. In real life it would be rare to find a market with freedom of entry/exit, identical products, price taking firms, etc. One point that could be made about the lack of super-normal profit is the lack of innovation. Innovation tends to be fueled by profit, without profit there is little room for firms to innovate. Innovation is one thing that can lead to a more efficient market, so in perfect competition once the efficient point is reached it will not be made any more efficient. Comprende?

Sam.

Principles of Economics: Profit Maximisation (Microeconomics)

Today's post will look at the profit maximisation for a firm. There really isn't that much too this, but I'll dedicate a post to it none the less. If you refer back to the post relating to a firm's revenue it will make what's about to be explained a lot easier. The main rule to remember here is that the profit maximising point for a firm is where the marginal revenue and marginal cost are equal. Why this point? Well, as long as marginal revenue is greater than marginal cost more profit can be made by increasing production. At the point where marginal revenue equals marginal cost, no more profit can be made and therefore this point will be the profit maximisation point.

Diagram time!

Profit maximisation is shown on this diagram here. We've set up a simple model of a firm's revenue and costs. Then, at the point MC = MR we have drawn a line up. This gives us two prices, P1 and P2. P1 is the actual market price for the good or service. P2 is the cost to produce that certain good. Therefore, using simple logic we can work out the actual price. P1 - P2 will give us the profit made on each good produced and then if we multiply this by the quantity we will have total supernormal profit. Or, visually it's the gold area on the diagram.

Notice I used the phrase supernormal profit. There are actually two levels of profit, normal profit and supernormal profit. Normal profit is the cost of staying in the industry; so this is essentially the minimum amount the firm needs to make in order to stop them leaving the industry. It will include such things as the pay for the entrepreneur. Supernormal profit is anything above this level, any additional income for the firm. A situation can also occur when the average cost curve is higher than the average revenue curve, if you picture this in your head and you'll see it'll result in a loss. In the short term some firms will not worry about this if they are using it as a technique to reduce competition or something similar. In this case nothing changes, the firm will still produce at the point MC = MR, however the only change is this time we'll call it the loss-mining position/quantity. 

Sorted! Profit maximsation and loss minimisation for you! Hope it helps, feedback and comments are of course always welcomed! Thank you guys, have a good evening.

Sam. 

Principles of Economics: Revenue (Microeconomics)

* Sorry about the delay with this post, I've had a busy week and have just got round to writing this up. But I'll have another one up tomorrow as well to make up for it. *

Right, today's post will be relating to revenue and more specifically a firms revenue. We'll start with a few of the basic bits of terminology that I'll be using throughout this post. Firstly, total revenue. This is fairly self-explanatory but I'll give a definition anyway. Total revenue is a firms total earnings in a period of time from the sale of a particular amount of goods, the formula is better known as price x quantity. Average revenue next and this is the amount a firm earns for each unit sold, the formula for this is (total revenue) / (quantity) which you may have noticed just equals price. Marginal revenue is the final term, this refers to the extra revenue gained from selling one more unit of a good. The formula for marginal revenue is (change in total revenue) / (change in quantity).

We'll first look at the revenue curves for a small firm. We'll be assuming this firm is in a perfectly competitive market (Will do a blog post on this later today/tomorrow). Basically, this means that the firms are generally too small to have any effect on the price of the good they are selling. If they raise their price no-one will buy from them, if they lower their price they will find an overwhelming demand and probably be charging less than the cost to produce the good. That being said, the market forces determine the price the firm has to charge.

As you can see here, the demand and supply have met in the market and this has created a price for the good. The firm, shown on the left has a demand curve of this price because consumers will only buy from the firm at this price. No matter the quantity, the price will remain the same. Another note on this, D = AR = MR because the price is constant. The average revenue and marginal revenue will always be the same because we are working with a constant price.  We can model the total revenue of a firm as well. This is simple, first we create a table with the quantity supplied, price and total revenue. We then plot this table. Simple.

Simple as that for a total revenue curve for a small firm. However, when it comes to larger firms and the price of the good does vary with output we are struck with a different scenario. The average revenue curve is still equal to the price and will be the demand curve, but this time it will be downward sloping as with the normal characteristic of demand. The marginal revenue curve will also be downward sloping, but at a faster rate than the average revenue curve and will more than likely reach negative values. This is due to the diminishing marginal rate of production, the marginal revenue falls with each additional good you produce up to a point where producing another good will generate no additional revenue and may even decrease revenue. Before the quantity where marginal revenue equals zero, the average revenue is elastic because an increase in quantity will lead to a rise in revenue. After this point, it's inelastic because a rise in quantity leads to a fall in total revenue. 

And all that's left to add to this is the shape of the total revenue curve when the price varies with output. I should note, this happens in larger firms when they can effect the market price. The total revenue curve would be somewhat hill shaped. It would slope up, reach a peak at some unknown point and then slop down again afterwards. You may be thinking "Ok, great... Why?"! Well, this will come in useful in the next posts when we look at profit maximisation of a firm. 

Thank you for reading again, keep watching for the next few posts which will relate and link to this one. Have a good day!

Sam.